Our Universe as a Dodecahedron

A direct link to the above video is at http://www.youtube.com/watch?v=Qu1GD_AifpM

Last time we talked about our universe within the omniverse. Now let's talk about the shape of our own universe.
This is an image of a rotating dodecahedron, from wikipedia. This unique platonic solid incorporates the golden ratio, which is often denoted by the Greek letter phi, usually lower case: φ. When you stack a number of dodecahedra together, interesting things happen with the way the different faces and vertices rotate: they can be seen to enfold one into another, and the resulting hints of rotating helix shapes, fractals, and the spirals found in nature link not just to the broad field of sacred geometry, but to cosmological theories about the structure of our universe.

These next two images come from a mind-blowing visualization tool you can download from http://geometrygames.org/: it's called Curved Spaces.
In entries like Poll 49 and Poll 58 we've talked about how our universe is not really flat and infinite, but rather slightly curved, making it finite but unbounded. In entries like An Expanding 4D Sphere and When's a Knot Not a Knot? we've also talked about the now-proven Poincaré Conjecture. Curved Spaces includes the Poincaré Dodecahedral Space mode pictured here, which lets you fly through the stacked dodecahedra that would form the surface of the 4D hypersphere our finite but unbounded universe resides within. And by putting a planet earth at the center of each dodecahdron, this fly-through gives us one way of visualizing how Everett's Many Worlds could be defined by our observation of the universe as a series of planck frames, one after another, each frame separate but connected to other possible adjacent frames: another favorite topic of this project.

In older entries like Everything and Seeing Eye to Eye, we've touched on the amazing ideas of Dan Winter, who continues to present an ever-growing body of work. As I've said before, Dan's web pages can seem overwhelming, but there's no denying his passionate pursuit of his ideas. The animated images we're looking at here come from Dan's gigantic goldenproof web page, which you'll see does include lots of graphics, animations, and movie clips if you scroll further down that page. The first two animations I've grabbed from Dan's website show the basic idea, which Dan describes this way:
"These visuals are graphed from my original equation of Golden Ratio on the correct conic dodeca stellation of how Hydrogen Radii- nest/embed into the PLANCK LENGTH (field coupling- to MAKE GRAVITY) - using GOLDEN RATIO - successful wave adding and multiplying (non-destructive compression)."

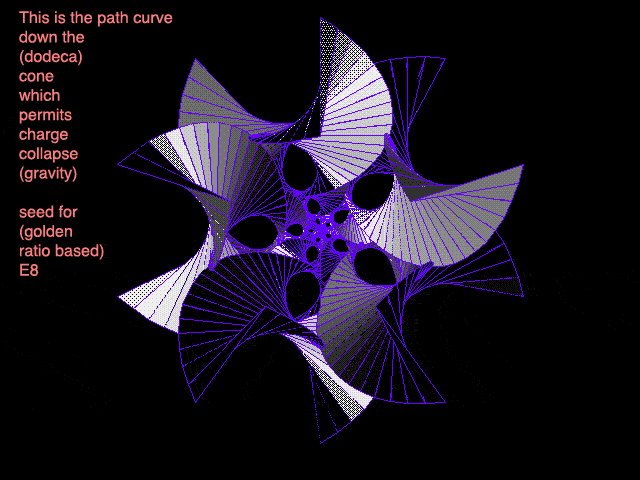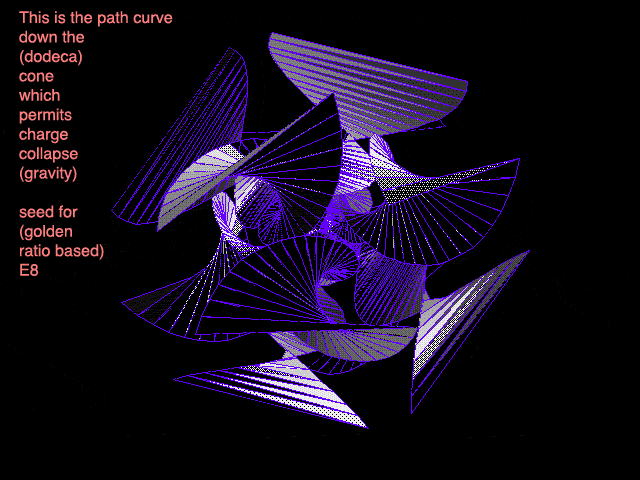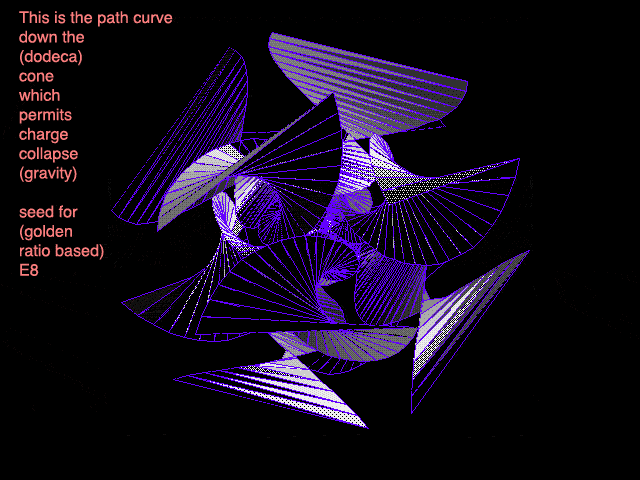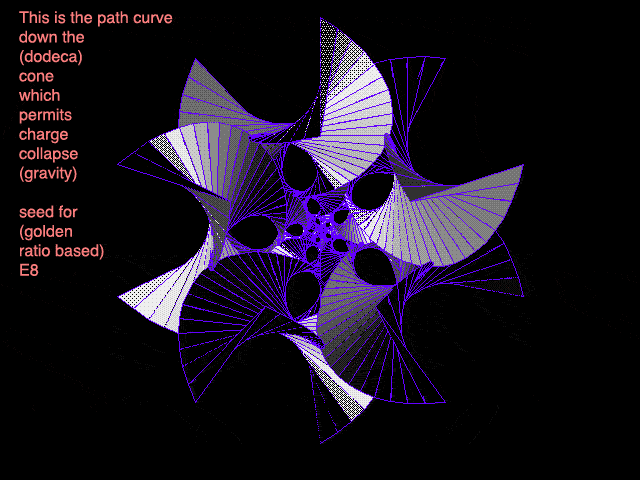As you know, the different electron shells of an atom are discrete - when an electron moves from one level to another, it doesn't travel through the intermediate space: it simply pops from one to the other, in a manner very similar to the "flatlander ant on a folded newspaper" concept we showed in the original tenth dimension animation. This is yet another example of how our reality, which seems continuous, is actually divided into tiny little "steps", or "frames" that are each one planck unit apart from the next: not just in space, but in space-time as well.

Dan quotes from The Golden ratio, ionic and atomic radii and bond lengths, a paper by Raji Heyrovska written in collaboration with J. Heyrovsky of the Institute of Physical Chemistry, Academy of Sciences of the Czech Republic, Prague. - The summary of the paper includes the following:

This work arose from the author's finding that the ratio of the radius of hydrogen, estimated recently (C.H. Suresh, N. Koga, J. Phys. Chem. A, 105, 5940 (2001)) by density functional methods, to the ground state Bohr radius is the Golden ratio, which operates in a variety of natural phenomena. It is found that the Golden ratio indeed plays a quantitative role in atomic physics.

Dan cites the above as confirmation of his own ideas about how important the golden ratio is to our fractal, enfolded reality. For me, this all ties back into the idea that our observed universe is being constructed one planck frame at a time by constructive interference occurring in the fifth dimension: which, as I've been saying from the outset of this project, is where our "now" is actually being observed from instant to instant, as it's chosen from a probability space of possible pasts and futures.

Let's look at one more interesting thing about a dodecahedron: it can be constructed from five pyramids, like so:

A tetrahedron is a four-sided pyramid, with each triangular face the same size. At left we see five interlocking tetrahdra. Each one is color-coded so it's easier to tell them apart, and these have been rotated to make all of their outer points equidistant from each other. As you can see in the right-hand image, these points can be joined by pentagons, and when we do so our old friend the dodecahedron emerges once again.

What's the point? We'll continue this discussion next time with Our Universe as a Point.

Enjoy the journey,

Rob Bryanton