Threes

A direct link to the above video is at http://www.youtube.com/watch?v=amcTK7Mnu70

This recently published video accompanies a blog entry from earlier this year called Three Becomes One. Our discussion this time also ties to a comment I made in Entangled Awareness and OBEs, where I suggested that we could think of my approach to visualizing the dimensions as a filing system that encompasses all possible expressions of information and reality.

Here's a link to a really great article written by Brian Hayes and published in a 2001 issue of American Scientist magazine: it's called Third Base. Please read the whole article, which celebrates the advantages of using the ternary (as opposed to the binary) counting system, which is really another aspect of the three becomes one concept. I did want to quote from a section I thought was particularly innovative: Brian's sub-heading for this section is "Martha Stewart's File Cabinet".

Some weeks ago, rooting around in files of old clippings and correspondence, I made a discovery of astonishing obviousness and triviality. What I found had nothing to do with the content of the files; it was about their arrangement in the drawer.

Imagine a fastidious office worker—a Martha Stewart of filing—who insists that no file folder lurk in the shadow of another. The protruding tabs on the folders must be arranged so that adjacent folders always have tabs in different positions. Achieving this staggered arrangement is easy if you're setting up a new file, but it gets messy when folders are added or deleted at random.

A drawer filled with "half-cut" folders, which have just two tab positions, might initially alternate left-right-left-right. The pattern is spoiled, however, as soon as you insert a folder in the middle of the drawer. No matter which type of folder you choose and no matter where you put it (except at the very ends of the sequence), every such insertion generates a conflict. Removing a folder has the same effect. Translated into a binary numeral with left=0 and right=1, the pristine file is the alternating sequence ...0101010101.... An insertion or deletion creates either a 00 or a 11—a flaw much like a dislocation in a crystal. Although in principle the flaw could be repaired—either by introducing a second flaw of the opposite polarity or by flipping all the bits between the site of the flaw and the end of the sequence—even the most maniacally tidy record-keeper is unlikely to adopt such practices in a real file drawer.

In my own files I use third-cut rather than half-cut folders; the tabs appear in three positions, left, middle and right. Nevertheless, I had long thought—or rather I had assumed without bothering to think—that a similar analysis would apply, and that I couldn't be sure of avoiding conflicts between adjacent folders unless I was willing to shift files to new folders after every insertion. Then came my Epiphany of the File Cabinet a few weeks ago: Suddenly I understood that going from half-cut to third-cut folders makes all the difference.

It's easy to see why; just interpret the drawerful of third-cut folders as a sequence of ternary digits. At any position in any such sequence, you can always insert a new digit that differs from both of its neighbors. Base 3 is the smallest base that has this property. Moreover, if you build up a ternary sequence by consistently inserting digits that avoid conflicts, then the choice of which symbol to insert is always a forced one; you never have to make an arbitrary selection among two or more legal possibilities. Thus, as a file drawer fills up, it is not only possible to maintain perfect Martha Stewart order; it's actually quite easy...

The protocol for avoiding conflicts between third-cut file folders is so obvious that I assume it must be known to file clerks everywhere. But in half a dozen textbooks on filing—admittedly a small sample of a surprisingly extensive literature—I found no clear statement of the principle.

Now, here's an article from the physorg.com website about a theory proposed in 2007 by mathematician George Sparling of the University of Pittsburgh that there are two additional dimensions beyond space-time which can be described as "time-like". Sound familiar? This is one way of describing the first six dimensions of my "new way of thinking about time and space". First, read the article, which includes mention of twistors and twistor space. It also includes Elie Cartan's "triality" symbol pictured here, which ties into the idea that Sparling's three time-like dimensions can be rotated into a single point (three becomes one), which can be thought of as a "null" or "zero" created by the perfectly balanced symmetry inherent within triality.

Interestingly, triality also connects to Garrett Lisi's E8 rotation, which we've talked about a number of times in this blog. Coincidentally, E8 as A Geometric Theory of Everything is a featured article in the December 2010 issue of Scientific American.

At the end of Three Becomes One I showed you the following two graphics:

Pictured at left: diagram showing congruence of null lines from Twistor Theory.
Pictured at right: diagram of Marko Rodin's Rodin Coil.
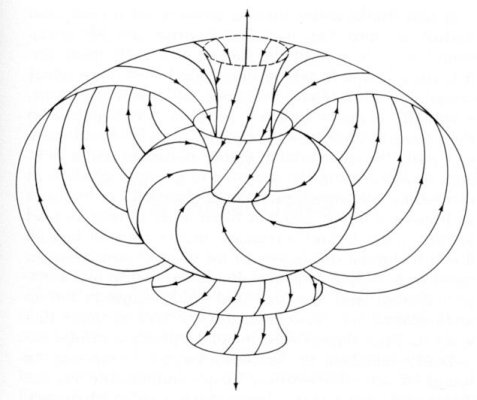
According to the June 2010 issue of Scientific American, there's renewed excitement about
Twistor Theory and String Theory being united by the highly respected theoretical physicist Ed Witten. It appears to me that this will all tie into the work of Marko Rodin, whose Rodin Coil is pictured at right, but that remains to be confirmed.

We're going to continue this exploration next time with an entry about Infinite Division. Till then, enjoy the journey!

Rob Bryanton